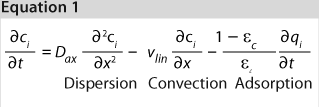Model-Assisted Process Development for Preparative Chromatography Applications

Process modeling is a core technology in biopharmaceutical production that ensures faster, safer processing and process development. Developing a model involves quite some work, so it is important to use the model efficiently. We describe an industry example of how a mechanistic model is best used under process development and how it increases process understanding and performance.

Present State of Process Development
Biopharmaceutical process development relies heavily on experimentation and previous experience expressed as “rules of thumb” and empirical correlations. This is a limitation when it comes to getting the most out of a process: Insufficient process knowledge makes a process run suboptimally. Problems that should be handled at-line are not, and batches are lost. Both industry and regulating agencies are working toward changing this state of affairs: The Food and Drug Administration’s (FDA’s) quality by design (QbD) initiative (1,2) and the International Conference on Harmonization’s (ICH’s) risk management guide (3) are helping this development. Process understanding is a central concept: Provided that manufacturers know their processes, critical process parameters, and functional relationships that link them to product safety and quality, then regulators allow greater flexibility.

PRODUCT FOCUS: ALL BIOLOGICS
PROCESS FOCUS: DOWNSTREAM PROCESSEING
WHO SHOULD READ: PROCESS AND PRODUCT DEVELOPMENT ENGINEERS KEYWORDS: PROCESS MODELING, PROCESS VARIATION, QBD, DESIGN SPACE LEVEL: INTERMEDIATE

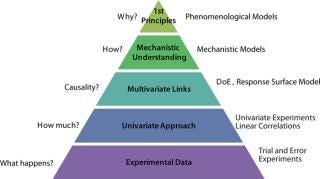
Modeling process development is a way to develop, document, and explore process understanding. Model complexity can range from linear correlations derived from univariate experiments to first-principles models based on molecular properties and thermodynamics (Figure 1). Model complexity also mirrors the level of process understanding, from models based on correlation to those based on cause-and-effect. Mechanistic models start from a conceptual understanding of chemical and physical processes (e.g., heat and mass transfer, chemical reaction rates, phase equilibria) that control a unit operation (e.g., reaction, mixing, separation). However, empirical fitting parameters are allowed so they keep model complexity at a manageable level and ensure that a model predicts the behavior of a process accurately.

Figure 1 

A mechanistic model can assist process development by guiding experimentation, investigating sensitivity to process parameters, and providing a quantitative measure of process robustness.

Model-Assisted Approach
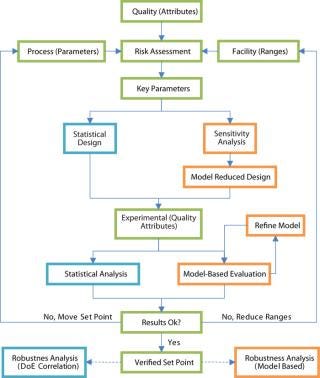
The model-assisted approach to process development is not free from experimentation. Experiments are performed and new information drawn from them. Figure 2 illustrates the contrast with a traditional, experimentcentered approach.

Figure 2

How It Works: First, calibration experiments are performed to identify model parameters. Then a model helps identify interesting parameter variations to study. In the classical approach, experimental design generates experiment points varying a few parameters that previous experience indicate are relevant. With a model, more parameters can be included in the first phase and eliminated on the basis of effects seen in model output. Experiments are interpreted according to responses predicted by the model, and discrepancies are identified as either experimental error or model inadequacy. In the classical approach, a statistical tool such as analysis of variance is used to rank parameters, but that does not provide information about causal relationships between parameters and process output. Interaction effects among more than two parameters remain unexplored because they would typically require an unfeasible number of experiments. However, interaction effects and nonlinearities are built into a process model and can be investigated freely, provided the model is detailed enough. Kaltenbrunner et al. describe a similar model-assisted approach (5). Their work used linear chromatographic theory, which limited the study to linear effects. What You Need: To build a process model, the objective must be defined. Determine the parameters to be included and the relevant outputs. Such information can be taken from the result of the risk analysis and a list of critical quality attributes (CQAs) set up during process design.

System boundaries and level of detail also must be defined. Requried details determin whether to model each unit operation separately or aggregate them. Separate models can be more detailed but also require more work. Aggregated models may help you assess the effect of disturbances and control choices on a larger scale. In our work, we use a model of an ion-exchange chromatography step.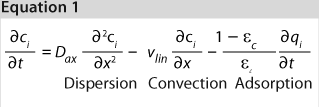

How It Relates to QbD: A mechanistic model consists of a mathematical description of changes taking place during the mode led process. In our current example, the model describes fluid flow through an ion-exchange chromatography column, dispersion, mass transfer from bulk liquid to particle surface, and adsorption kinetics. Surrounding equipment such as mixing tanks and product pooling are also modeled. Model parameters describe the effects of process parameters such as salt concentration, pH, flow rate, and protein concentration on the modeled phenomena and therefore link process parameters to quality, safety, and performance attributes of the process output. Such a model constitutes process understanding according to ICH definition and is considered a summary of available process knowledge (6). Process design space is the multivariate parameter space for process operation inside which a process is expected to meet quality requirements. A mechanistic model enables a wide definition: Process design space is defined by the model output being within the limits of quality attributes. Having a design space defined by a model instead of univariate acceptable ranges is essential to using the full potential of QbD (7).

An Example from Industry
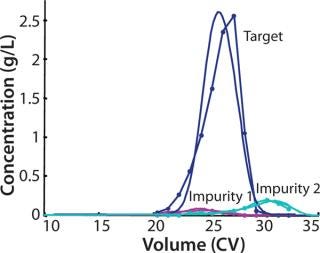
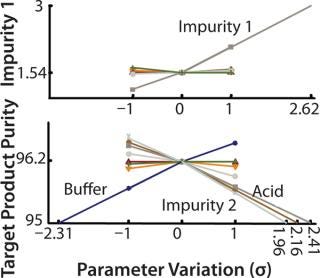
Model-based methods are applied to process validation of an industrial ion-exchange chromatography step, separating the active component from product related impurities eluting before (impurity 1) and after (impurity 2) the main peak (Figure 3). When a process is transferred from development to production, it should be challenged by changing process conditions within the normal operating range. The purpose of that process challenge is to validate the operating point by demonstrating process robustness and identifying critical process parameters and their proven acceptable ranges.

Figure 3

Figure 4

Figure 5

Figure 6: 

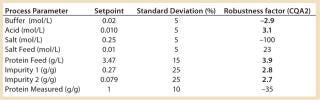
We used the MATLAB program from MathWorks, Inc. www.mathworks.com) to construct a model of a chromatography step together with buffer preparation before and product pooling after the column. A homogenous convective–dispersive model describes mass transport in the chromatographic column, and a simplified self-association isotherm describes adsorption kinetics (8) (Equations 1, 2). The model was discretized in space with the finite-volume method and solved with a MATLABs ode15s solver. We calculated purity and yield of the process using numerical integration of the concentration vector between the selected cut points. Risk analysis identified eight process parameters and their respective variability, which we included in our analysis. Table 1 lists the parameters, setpoints, and distributions. CQAs in the process were the the amount of impurity 1 in the product (CQA 1 <3%) and target product purity (CQA 2 >95%).

Table 1: Process parameters and estimated variability included in the study; robustness factors in relation to target product purity are included; critical parameters indicated in bold type.

Table 1: Process parameters and estimated variability included in the study; robustness factors in relation to target product purity are included; critical parameters indicated in bold type. ()

Critical Process Parameters: The model tested effects on the CQAs of variations in each parameter up and down one standard deviation. A large effect indicates that a process is sensitive to a parameter or that the variance of the parameter is large. That is quantified by calculating robustness factor, which is the change — measured in standard deviations — in a parameter that is required to cause an out-of-specification batch. The smaller the robustness factor, the more sensitive a process is to a given parameter. Five parameters had effects of comparable strength on CQA 2, whereas CQA 1 only was sensitive to one parameter: the amount of impurity 1 in the feed. So the reduction of impurity 1 is unsatisfactory for high levels in the feed. Robustness factors can be used to design a model-reduced experimental plan that will verify (experimentally) important parameter variations.

A “worst-case corner” at a desired probability level is found, and if the experiment at this point fulfills quality requirements, then a process is considered robust. We studied interaction between significant process parameters by making simulations in a ful l-factorial design. Results confirmed that the amount of impurity 1 was the only significant parameter for CQA 1 and revealed a synergy between the amount of impurity 2 and the buffer and acid concentrations. Lower pH decreased the removal of impurity 2, indicating that pH should be high enough. There was also an interaction effect between buffer and acid, which we expected because both influence pH by means of the acid–base equilibrium included in our model.

Robustness
Experiments can be expensive and time-consuming to perform. They are subject to uncertainties that make it impossible to know the exact values of studied parameters. That makes experiments an unsuitable method to investigate the effect of variations inside a narrow operating range. Simulations, however, are inexpensive and fast to perform, and they repeat the exact parameter values that are provided to a model.

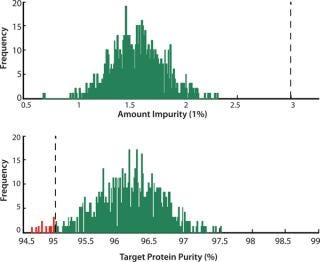
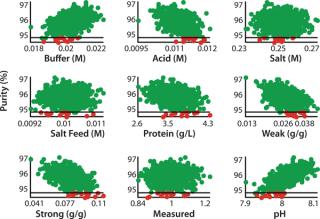
So a statistically relevant robustness analysis can be performed by generating a large amount of process scenarios with random variations in process parameters. Scenarios are simulated and the distribution of the CQAs indicate process robustness. Out of 800 simulated batches, 12 batches failed (1.5%), all because of too low a target purity (Figure 5). The process can be said to be robust at a 95% level, but in practice we may want a better result than this. We plotted CQA 2 against process parameter values in all simulated batches and studied for trends (Figure 6). In addition to the studied parameters, other factors can be studied in the same way, because all information is available in the model output. Because pH is affected by the levels of both buffer and acid, it appears to have a strong effect of CQA 2 (visible by the narrow band of scatter points and that all failed batches lie at the lower half of the parameter range). To improve robustness with respect to CQA 2, the pH of the wash and elution buffers should be monitored and controlled.

Expanding Process Knowledge
We have shown how a mechanistic model can be used to aid process development, in particular a process challenge aiming to identify critical process parameters and demonstrate process robustness. Our model both summarizes and expands existing process knowledge because it can be used to explore process settings and variables. New effects can be added as information becomes available and results are refined. Our model analysis, once a methodology has been chosen, is easily repeated for more parameters, new ranges, or at a new setpoint. It can therefore be of use postapproval for process support, when changing a facility, or for optimizing a process.

This model can assist in choosing experiments, thereby ensuring that work and resources are well-spent. Parameters with little or no effect, or variations in a direction that does not reduce quality should not be investigated more than to validate a model result. With our model in place, it is also easy to study parameters that would have been hard or impossible to study experimentally. We found the amount of impurity 1 in the feed to be a critical factor. In an experimental study, only a few batches of feed would typically be used, so that effect would have gone unnoticed. That is, the model-assisted approach had the direct benefit of detecting a critical source of variability that must be monitored in our process.

Benefits of a Process Model

Experimental robustness analysis is based on investigating the “worst-case corner.” With many critical process parameters, as is the case for CQA2, this becomes an extremely conservative approach because the probability of them all varying at the same time is small. Furthermore, experimental uncertainty makes the results unreliable. With our model, which can simulate a batch in a matter of seconds or minutes, it is possible to evaluate a large number of process scenarios and obtain a quantitative measure of the probability of batch failure. All information regarding simulated batches is stored and can be analyzed for other parameters than what was first conceived.

We illustrated that with the case of pH, which was included as a secondary parameter. Results show how our model adds to process understanding when data are analyzed. In addition, new process settings such as an alternative pooling strategy can be investigated when the need arises. It is important that a process model is based on good experimental data and sound scientific principles, or the model results will not be reliable. Evaluate model quality in context with experimental quality and model application. Although testing efforts are not necessarily reduced, they will be directed to the most useful operating points, to extract the most information possible.

About the Author

Author Details Karin Westerberg is a PhD student in the department of chemical engineering at Lund University. Ernst Broberg Hansen is principal scientist at Novo Nordisk A/S, Bagsværd, Denmark; Thomas Budde Hansen is principal scientist and Marcus Degerman is a research scientist at Novo Nordisk A/S, Gentofte, Denmark. Corresponding author Bernt Nilsson, is a professor at Department of Chemical Engineering, Lund University, PO Box 124, SE-221 00 Lund, Sweden, 46 46 222 49 52, 46 731 58 35 75; [email protected].

REFERENCES

1.) ICH 2005. Q8: Harmonized Tripartite Guideline: Pharmaceutical Development.

2.) ICH 2008. Draft Consensus Guideline: Pharmaceutical Development Annex to Q8.

3.) ICH 2005. Q9: Harmonized Tripartite Guideline: Quality Risk Management.

4.) Julien, C, and W.A Whitford. 2008. New Era for Bioprocess Design and Control, Part 1. BioProcess Int. 6:S16-S23.

5.) Kaltenbrunner, O. 2007. Application of Chromatographic Theory for Process Characterization Towards Validation of An Ion-Exchange Operation. Biotech. Bioeng. 98:201-210.

6.) Gernaey, KV. 2010. Application of Mechanistic Models to Fermentation and Biocatalysis for Next-Generation Processes. Trends Biotechnol. 28:346-354.

7.) García-Muñoz, S, S Dolph, and HW. Ward. 2010. Handling Uncertainty in the Establishment of a Design Space for the Manufacture of a Pharmaceutical Product. Comput. Chem. Eng. 34:1098-1107.

8.) Mollerup, JM. 2008. A Review of the Thermodynamics of Protein Association to Ligands, Protein Adsorption, and Adsorption Isotherms. Chem. Eng. Technol. 31:864-874.