Practical Applications of Process Capability Indices in the Biopharmaceutical Industry: A Simulation-Based Study

HTTPS://STOCK.ADOBE.COM

Process capability often serves as a metric for quantifying biomanufacturing-process performance. The term refers to the extent of variation in measurable property X of a given biological product made by a given process relative to the width of that property’s specification limits. Thus, process capability provides insight into how consistently a manufacturing process generates products that meet specifications. In other words, the higher the process capability is, the lower the probability is for an out-of-specification (OoS) outcome.

Evaluating process capability is particularly important in biopharmaceutical manufacturing. Multiple analytical results (often with multiple replicates) are generated routinely for release of drug-product batches — hence the need to ensure consistent process performance and product safety and efficacy.

Definitions: Statisticians working in industry and academia have proposed several process-capability indices (1). Equations 1–3 list the most basic indices for a process with an upper specification limit (USL) only, a process with a lower specification limit (LSL) only, and a process with both upper and lower specification limits, respectively. The indices assume that a biomanufacturing process generates a biological product with property X, values for which follow normal distribution and have a mean of μ and a variance of σ². If a process is centered, meaning that it has a distribution mean at the center of the specification limit interval, then C_pk, C_pl, and C_pu values are equal.

Equations 1–7: Basic calculations for process-capability indices.

A process-capability index also can be understood as a quantification of the extent of observed process variation compared with the allowable amount of process variation within specification limits (Figure 1). Popular commercial software tools such as the JMP package sometimes present alternative process-capability indices: e.g., P_pk, P_pu, and P_pl. The difference between the P_pk and C_pk sets of indices lies primarily in their calculation of variability (σ).

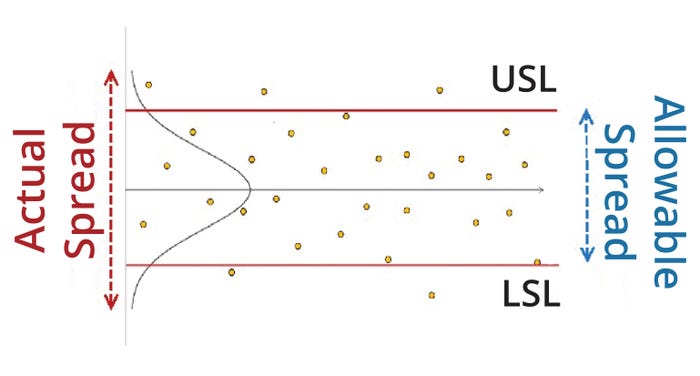
Figure 1: Schematic for a typical biomanufacturing process with an upper (USL) and lower specification limit (LSL).

Because of the relatively high variability of biological-assay results, some drug attributes necessitate testing with multiple replicates for each batch. That practice creates subgroupings in the resulting data. In such cases, two kinds of variability can be calculated: within-subgroup variability (also called short-term σ) and overall variability (long-term σ). C_pk calculation is based on within-subgroup variability, whereas P_pk is calculated using overall variability. In the absence of subgrouping, the C_pk and P_pk sets of indices have no significant differences.

Calculation Methods for Nonnormal Distributions: Process-capability calculations are relatively straightforward for normally distributed data. However, if data do not follow normal distribution, then standard capability definitions might generate misleading results because those definitions assume normality. Therefore, several methods have been proposed in literature to address the issue of nonnormality (2, 3). Each technique has merits and limitations.

Percentile/quantile-based methods (4) and z-score (nonconformance) methods (5) are used frequently for process-capability calculation for nonnormal data. As the name suggests, percentile-based methods leverage percentiles instead of σ values (Equation 4). In a normal distribution, x_0.5, x_0.99865, and x_0.00135 are equivalent to μ, (μ + 3σ), and (μ – 3σ), respectively.

The percentile method is a general approach that can be used for any kind of distribution. However, its major drawback is its potentially misleading interpretation of process capability. A process-capability index provides a simple measure of the probability of OoS results. For normally distributed and centered process data with both USLs and LSLs, P_pk = 1 is equivalent to an OoS risk of 0.27%. But the relationship between P_pk and %OoS is invalid when a percentile-based method is used. Thus, the same P_pk value corresponding to different fitted distributions will result in different %OoS values.

The z-score method provides the same %OoS result for a specific P_pk value regardless of the type of fitted distribution. This method leverages the quantile function of the standard normal distribution to calculate equivalent limits that would yield the same probability on a standard normal scale.

Equations 5–7 show how to calculate an equivalent USL (USL_eq), an equivalent LSL (LSL_eq), and a process-capability index, respectively, for a given nonnormal probability distribution described by probability density function (PDF) f(x). Therein, F(x) represents the cumulative distribution function (CDF) corresponding to f(x), and Φ^–1 is the quantile function for a standard normal distribution.

Power-transformation methods such as the Box–Cox (6) and Johnson techniques (7) also can be used to transform nonnormal distributions to normal distributions, enabling application of standard formulas for process-capability calculation.

Focus of Current Work: Any of the above methods can be applied easily for process-capability calculation with the help of commercially available statistical-analysis software. However, selecting an appropriate method is generally not a straightforward process. Selection is especially challenging in cases with limited amounts of data because of the inherent difficulty in fitting the appropriate distribution. The biopharmaceutical industry often encounters such issues because of time-consuming experiments, high experimentation costs, and limitations on patient availability for clinical trials. Despite data-availability constraints, analysts must make critical decisions about manufacturing processes. Therefore, statistical methods must be selected to address such limitations. Herein, one of our goals is to compare the performance of process-capability calculation methods presented above for small data sets using simulations.

In cases with subgrouped data, process-capability evaluation requires even more attention than usual. As mentioned above, two kinds of indices can be calculated for such data. Depending on the type of variability applied during calculation, the methods’ interpretations of process capability can differ. For instance, consider cases in which multiple replicates from the same batch are tested to provide an average result. Per regulatory guidance, both the individual and averaged results must be compared against the respective specification limits (8). The overall OoS risk increases because values from multiple replicates are up for comparison.

Process-capability index calculation is not straightforward in such cases because more than one type of variability can be considered for calculation. If only assay variability is considered, then the resulting process-capability index will indicate the assay’s performance but not that of the manufacturing process. On the other hand, using only batch-to-batch (process) variability is insufficient too because increased %OoS risk for a given batch comes primarily from the differences in the replicates’ values. Total variability (the sum of assay and process variability) can provide an alternative for process-capability calculation. However, that method does not account for the number of replicates. Thus, that formula for process-capability calculation should not be used in cases with subgrouped data. Our second objective in this article is to propose a mathematical framework for determining %OoS risks when individual replicates are compared against specification limits.

Methods

Simulation Approach for Comparison of z-Score and Percentile Methods: Below, we focus on the widely used z-score and percentile methods for process-capability evaluation in the case of nonnormal data distribution. We compare the methods’ performance under the constraint of small data samples. Because real-world process-capability data are generally unknown within the biopharmaceutical industry, we strategically generated synthetic data for our comparisons.

For normally distributed data, both methods yield the same process-capability index. Therefore, only data with nonnormal distributions require comparison. Index calculation also requires specification limits. Considering those factors, we developed the following simulation-based procedure to compare z-score and percentile method performances for nonnormally distributed data:

1 — Select a nonnormal distribution with defined distribution parameters.

2 — Calculate specification limits for the given coverage factor (c) or for the corresponding percentiles of the nonnormal probability distribution using a PDF. For example, a coverage factor of 2 is equivalent to a USL at the 97.5th percentile and an LSL at the 2.5th percentile.

3 — Generate sample set of size n using a nonnormal PDF with parameters defined in the first step.

4 — Using the calculated specification limits, calculate process-capability indices using z-score and percentile methods.

5 — Calculate the difference (∆) between the two indices.

6 — Repeat steps 4–6 k times to generate the distribution of ∆.

7 — Repeat all of the above steps for the same type of distribution but with different distribution parameters so that higher-order scaled moments (e.g., skewness and kurtosis) can be varied.

In our study, we varied skewness but not kurtosis because both sets of values correlated strongly and had similar effects on the distribution of the difference (∆) (see Appendix).

Process-Capability Evaluation for a Multiple-Replicate Testing Scenario: As mentioned before, analysts sometimes need to test multiple replicates for drug attributes at a given stage of a biopharmaceutical process — e.g., when using samples from drug-substance intermediates, drug substances, and final drug products. In cases with multiple replicates per batch, the %OoS risk for a batch equals the probability of having at least one replicate falling outside specification limits. As the number of replicates per batch increases, the %OoS risk increases because of assay variability. A batch’s %OoS risk also depends on manufacturing-process variability.

Variability Breakdown Analysis: Because %OoS risk depends on both sources of variability, the overall variability observed across multiple batch results for a specific assay must be broken down into process and assay variabilities. Variance component analysis (VCA) is the standard statistical approach for partitioning overall variability (9). For batches tested over multiple experimental setups with multiple replicates per setup, VCA can break down the total variability into process- and assay-variability components.

OoS Risk Evaluation: Figure 2 presents distributions of mean-attribute and individual-measurement values. Overall, process mean (µ) can be estimated as the average of individual-batch averages. Process (σ_p) and assay (σ_a) variability can be estimated using VCA.

Figure 2: (LEFT) Mean attribute distribution with an overall process mean of μ, process variability of σ_p, and a process mean μ_i for the randomly selected ith batch; (RIGHT) distribution of a measured attribute’s individual values for the ith batch, with an assay variability of σ_a and an upper (USL) and lower specification limit (LSL).

For an attribute with single result y, the %OoS risk for the ith batch is the conditional probability of y being outside specifications given the batch mean (µ_i). Graphically, that is the area of the distribution outside the USL and LSL (Figure 2, right). %OoS risk is calculated using Equation 8, in which CDF denotes a cumulative distribution function.

Equations 8–11: Calculations of risk for a biomanufacturing process generating a product with an out-of-specification (OoS) attribute.

However, %OoS risk needs to be adjusted to account for the multiple-replicates scenario. Assuming that each replicate for the ith batch tested is an independent Bernoulli trial and that the probability of a within-specification result equals (1 – OoS_i(µ_i)), then the probability of at least one replicate falling outside of specification is given by Equation 9. Assuming that the measured attribute (y) follows normal distribution, that expression can be described further using a CDF for normal distribution (Equation 10).

Estimation of overall average OoS risk requires summation over all possible realizations of the ith batch, as shown in Equation 11. Therein, Prob(m) represents the probability density function of a normally distributed process. Note that %OoS risk must be evaluated numerically because Equation 11 is not amenable to an analytical solution.

Results and Discussion

Here, we describe application of our simulation approach to compare the two process-capability calculation methods for small sets of nonnormally distributed data. Then, we evaluate %OoS risks for multiple-replicates testing scenarios using the mathematical framework discussed earlier.

Comparison of z-Score and Percentile Process-Capability Indices: Several types of nonnormal distributions are described in statistics literature. A general evaluation of all such types is impossible, so we selected log-normal and Weibull distributions as two representative types. We chose the former option for a couple of reasons. When an attribute is log-normally distributed, logarithmic transformation of that attribute results in normal distribution. Logarithmic transformation also is among the most frequently used nonlinear transformation methods in the biopharmaceutical industry (10, 11). Regarding Weibull distribution, a three-parameter technique can be applied to represent exponential, Rayleigh, generalized-gamma, generalized–extreme-value, and other types of nonnormal distributions.

Table 1 summarizes the parameters used in our simulation-based comparison of z-score and percentile methods for process-capability index calculation. Distribution parameters were varied in such a way that skewness of the distribution lies in {0.3 to 7}. Using the two sets of specification limits and two types of distributions, we conducted a total of four simulation studies.

Table 1: Simulation parameters for comparing z-score and percentile methods; c = coverage factor, k = shape, n = number of samples, μ = location, σ = scale, λ = scale, θ = location

Log-Normal Distribution: Figures 3 and 4 illustrate simulation results for log-normal distribution for specification limits based on coverage factors of 3 and 2, respectively. In both cases, the absolute median difference (∆) between the two capability-calculation methods increased with increases in skewness. Values for ∆ increased at a much faster rate under a coverage factor of 2.

Figure 3: Boxplot illustrating the distribution of differences (Δ) between percentile- and z-score–method estimation of processcapability indices (P_pk) at increasing values of skewness for simulated log-normally distributed data; limits for determining out-of-specification (OoS) results were based on three standard deviation limits.

Figure 4: Boxplot illustrating the distribution of differences (Δ) between percentile- and z-score–method estimation of processcapability indices (P_pk) at increasing values of skewness for simulated log-normally distributed data; limits for determining out-of-specification (OoS) results were based on two standard deviation limits.

For specification limits based on a coverage factor of 3, P_pk values obtained by the percentile and z-score methods ranged from 0.80 to 0.89 and from 0.89 to 0.92, respectively. Similarly, for specification limits based on a coverage factor of 2, P_pk ranged from 0.23 to 0.48 and from 0.51 to 0.52, respectively.

Weibull Distribution: Figures 5 and 6 illustrate simulation results for Weibull distributions with specification limits based on coverage factors of 3 and 2, respectively. In both cases, once again, ∆ values between the two process-capability calculation methods increased with increases in skewness.

Figure 5: Boxplot illustrating the distribution of differences (Δ) between percentile- and z-score–method estimation of processcapability indices (P_pk) at increasing values of skewness for simulated Weibull-distributed data; limits for determining out-of specification (OoS) results were based on three standard deviation limits.

Figure 6: Boxplot illustrating the distribution of differences (Δ) between percentile- and z-score–method estimation of processcapability indices (P_pk) at increasing values of skewness for simulated Weibull-distributed data; limits for determining out-of specification (OoS) results were based on two standard deviation limits.

For specification limits based on a coverage factor of 3, P_pk values from the percentile and z-score methods ranged from 0.62 to 0.89 and from 0.88 to 0.94, respectively. Similarly, for specification limits based on a coverage factor of 2, values from the percentile and z-score methods ranged from 0.19 to 0.53 and 0.44 to 0.52, respectively.

Findings: We made the following observations based on those four case studies. The first point concerns the median estimate of the absolute difference (Δ) in P_pk values, with Δ values increasing alongside larger skewness values. Skewness measures the asymmetry of the probability distribution of a random variable around its mean. Skewness has a zero value in cases of normal distribution and a nonzero value for nonnormal distributions. Therefore, we can conclude that the difference (Δ) in P_pk values becomes larger as the extent of nonnormality increases.

Because of a small sample size, we observed a spread in the P_pk values. Values obtained from the z-score method were spread less widely relative to values from the percentile method, indicating that the z-score method is more robust. The wider spread in percentile-method P_pk values can be attributed to the percentile calculations (x_0.99865 and x_0.00135), which are influenced significantly by the small sample size.

We set specification limits such that %OoS could be controlled. Theoretically, %OoS would be 5% and 0.27% under coverage factors of 2 and 3, respectively. We observed a range of P_pk values in simulations for a given coverage factor, but all P_pk values corresponded to the same theoretical OoS risk. In general, a process-capability index ≥1.0 is desirable for a normally distributed process. That result corresponds to an OoS risk of 0.27% for two-sided limits. In cases of nonnormal (log-normal and Weibull) distributions with specification limits based on a coverage factor of 3, both methods yielded median P_pk values <1.0. The minimum P_pk value for Weibull distribution based on the percentile method was 0.62. That value was achieved for a highly skewed distribution. The significant disparity between the expected (1.0) and estimated P_pk values (0.62) reflects the limitations of the percentile method for highly skewed distributions.

The same conclusion can be drawn for specification limits based on a coverage factor of 2. The expected P_pk value was 0.67, but the percentile-based minimum estimated P_pk value for a Weibull distribution was only 0.19. On the other hand, z-score–based P_pk values were much closer to the expected values, ranging from 0.88 to 0.94 (expected P_pk = 1.0) and from 0.44 to 0.52 (expected P_pk = 0.67) for coverage factors of 3 and 2, respectively.

In summary, z-score–based P_pk values for a nonnormal distribution carry the same meaning as P_pk values for a normal distribution because the relationship between P_pk and %OoS remains intact. The relatively small differences observed between the expected and calculated P_pk values could be due to a small sample size.

Multiple-Replicates Testing Scenario: Based on the methodology that we set out earlier, we conducted simulations to illustrate the limitations of traditional process-capability calculations. As we mentioned, %OoS is a more appropriate metric for evaluating process capability than the traditional process-capability indices (e.g., C_pk and P_pk) in cases when multiple replicates are tested. Table 2 lists the parameters that we used for simulation. We set specification limits such that the %OoS for a single-replicate testing scenario would be 5%.

Table 2: Simulation parameters for comparing z-score and percentile methods; c = coverage factor, k = shape, n = number of samples, μ = location, σ = scale, λ = scale, θ = location

Figure 7 shows calculated overall %OoS values corresponding to several simulated scenarios. As expected, %OoS values for single-replicate testing scenarios were ~5% in all cases, whereas %OoS became larger with increases in assay variability for multiple replicates (n_rep > 1). The %OoS also increased with larger numbers of replicates.

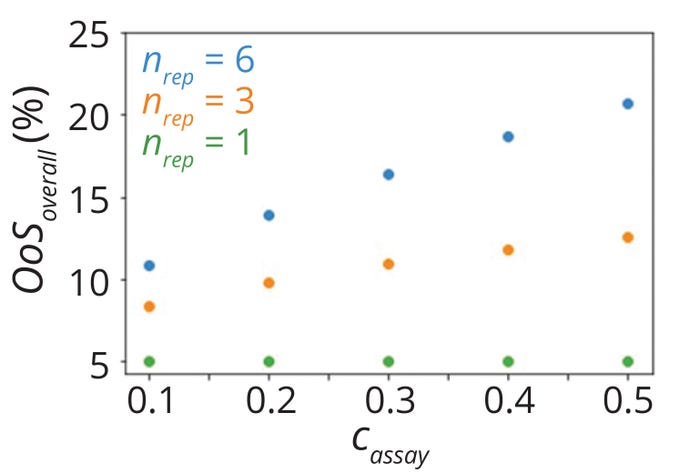
Figure 7: Overall risk of out-ofspecification results (%OoS) values for parameters listed in Table 2.

In single-replicate testing, an OoS risk of 5% corresponds to a C_pk value of 0.667 for normally distributed data. Because the traditional method of process-capability calculation does not account for the number of replicates, it yields the same C_pk (0.667) even for scenarios with multiple replicates (n_rep > 1). Thus, it overestimates process capability in cases with multiple replicates. Differences in estimates between the traditional and proposed methods become larger with increases in both the number of replicates and the proportion of overall variability due to assay performance.

Conclusion

Our purpose in this article was to address some practical challenges related to process-capability calculations for biopharmaceutical-manufacturing processes. Specifically, we wanted to address the fact that measured attributes do not always follow normal distribution. Therefore, a reliable and interpretable method is needed for process-capability evaluation. The z-score method not only generates robust estimates for process-capability indices for nonnormal distributions, but also preserves the relationship between process-capability indices and OoS rates. Outcomes from our simulations highlighted limitations of the percentile method for process-capability calculation for nonnormal distributions. Therefore, we recommend using the z-score method for such cases.

We also introduced a mathematical framework for process-capability evaluation for situations in which individual results for an attribute are subjected to specification limits in addition to average results. Although our proposed analytical solution applies to normal distributions, it can be extended to nonnormal distributions using numerical computations.

References

1 Montgomery DC. Introduction to Statistical Quality Control (Eighth Edition). John Wiley & Sons: New York, NY, 2019.

2 McCormack DW, Jr., et al. Capability Indices for Non-Normal Data. Qual. Eng. 12(4) 2007: 489–495; https://doi.org/10.1080/08982110008962614.

3 Tang LC, Than SE. Computing Process Capability Indices for Non-Normal Data: A Review and Comparative Study. Qual. Reliab. Eng. Int. 15(5) 1999: 339–353; https://doi.org/10.1002/(SICI)1099-1638(199909/10)15:5%3C339::AID-QRE259%3E3.0.CO;2-A.

4 Statistical Process Control. Automotive Industry Action Group, 2024; https://www.aiag.org/quality/automotive-core-tools/spc.

5 Bothe DR. Measuring Process Capability: Techniques and Calculations for Quality and Manufacturing Engineers. McGraw-Hill: New York, NY, 1997.

6 Box GEP, Cox DR. An Analysis of Transformations. J. Royal Stat. Soc. 26(2) 1964: 211–243; https://doi.org/10.1111/j.2517-6161.1964.tb00553.x.

7 Johnson NL. Systems of Frequency Curves Generated by Methods of Translation. Biometrika 36(1–2) 1949: 149–176; https://doi.org/10.2307/2332539.

8 CDER. Investigating Out-of-Specification (OoS) Test Results for Pharmaceutical Production: Guidance for Industry. US Food and Drug Administration: Silver Spring, MD, 2022; https://www.fda.gov/media/158416/download.

9 Ott RL, Longnecker M. An Introduction to Statistical Methods and Data Analysis (Sixth Edition). Brooks/Cole: Pacific Grove, CA, 2010.

10 USP <1010>. Analytical Data-Interpretation and Treatment. US Pharmacopeial Convention: Rockville, MD, 2024.

11 USP <1032>. Design and Development of Biological Assays. US Pharmacopeial Convention: Rockville, MD, 2024.

12 Johnson NL, Kotz S, Balakrishnan N. Continuous Univariate Distributions, Vol. 1 (Second Edition). Wiley-Interscience: Hoboken, NJ, 1994.

Corresponding author Shyam Panjwani is principal data scientist, and Konstantinos Spetsieris is head of data science and statistics at Bayer US, LLC, 800 Dwight Way, Berkeley, CA 94710; [email protected]. Now at Genentech, Darrick Shen was a data scientist at Bayer US. Data supporting the findings of this study are available from the corresponding author upon reasonable request.