Bioconjugates represent an important and growing class of pharmaceuticals that include PEGylated proteins, vaccines, and antibody-drug conjugates (ADCs) (1–8). Numerous protein conjugation techniques exist (9). Among the more important conjugation chemistries used for protein therapeutics are N-hydroxysuccinimide (NHS), aldehyde, and maleimide (10–13).
To date, process development of industrial biopharmaceutical conjugation reactions has largely been empirical in nature. Typically, many experiments testing different reaction parameters are required to identify optimal process conditions. In some instances, nonmechanistic statistical models can be used, often using JMP or similar software. However, such mathematical descriptions can suffer from a number of deficiencies. In particular, it is difficult for a statistical model to fully capture the complex dynamic behavior seen for many multistep conjugation reactions and hence allow limited extrapolation.
Kinetic models have shown promising results to accurately predict bioconjugation reactions (14–16). Kinetic models may prove particularly useful for ADCs. Due to the high cost and toxic nature of ADC payload reagents, there is tremendous incentive to limit their use during process development. Although chemical reaction engineering is routinely used in many industries, it has seen limited application in industrial bioconjugation process development. Two factors contribute to this limitation: First, biomolecules in industrial bioprocesses are highly complex. Second, many bioconjugation reactions are described by a system of nonlinear ordinary differential equations (ODEs) that require numerical integration.
In the literature, the integration has often been performed using numerical computation software packages with built in ODE subroutines such as MATLAB or MicroMath (14, 16). Although such tools are extremely powerful, they are not dedicated chemical kinetics solvers. As a result, process developers must translate reaction mechanisms into a system of ordinary differential equations, enter those equations as code the software can compile, and then numerically integrate them using an appropriate ODE solver.
Here we describe a flexible bioconjugation reaction engineering simulator using an open-source Java kinetics package named Tenua (17). This software is freely distributed online under the Sun public license. The approach does not require a detailed understanding of numerical methods or differential equations. Rather, it requires only basic knowledge of chemical kinetics and the ability to define reaction mechanisms. As such, it is accessible to a wide group of process development professionals. We describe program functionality and provide several worked examples based on kinetic models and rate constants found in other literature. Finally, we provide experimental data for a multiconjugation PEGylation reaction with corresponding modeling results. Code for all examples in this work is provided as supplementary materials online with this article.
Materials and Methods
Software: We used the open-source chemical kinetics software package Tenua (17) for all simulations. The program (available as an executable Java archive file) is freely distributed online. Tenua software is based on an earlier kinetics package called KINSIM (18), which has been ported to the Java programming language.
With Tenua software, reaction mechanisms are input using chemistry notation. The software automatically generates and solves the resulting system of ODEs. Numerical integration for nonstiff systems is performed using the Bulirsch-Stoer algorithm. Stiff systems can be solved using the Bader-Deuflhard algorithm. Tenua requires Java Runtime Environment (JRE) software, which is available free from Oracle (19). (Some operating systems automatically change the file name extension of Java archive files (.jar) to that of a zip file to view the contents. This can be remedied by manually renaming the extension to jar.) In the current work, simulation data were exported to Microsoft Excel software to generate kinetic plots.
Chemicals: We obtained hen egg white lysozyme and sodium cyanoborohydride (NaCNBH3) from Sigma–Aldrich (St. Louis, MO). We purchased l-lysine hydrochloride, sodium sulfate, hydrochloric acid, ethanol, sodium phosphate monobasic and dibasic from JT Baker. We purchased methoxy-PEG-propionaldehyde (mPEG-aldehyde) with an average molecular weight of 20kDa from NOF Cooperation (Tokyo, Japan).
PEGylation Reaction Conditions: We carried out PEGylation of lysozyme in 25 mM sodium phosphate buffer, pH 7.0 at room temperature. Protein concentration was 4 mg/mL with a 5× molar excess of the PEG reagent. Sodium cyanoborohydride was added to a concentration of 20 mM. We took samples at fixed intervals and quenched the reaction by immediate addition of a 0.1M lysine solution. mPEG-aldehyde reacts with amine groups, and reaction products with varying degrees of PEGylation (mono, di-, tri-, etc) are generated.
Analytical Methods: We monitored the reaction progress using size-exclusion chromatography (SEC) analysis of the quenched samples on a Zenix SEC 300 column from Sepax Technologies, Inc. (Newark, DE). The SEC running buffer consists of 100 mM sodium sulfate, 100 mM sodium phosphate, and pH 6.8 buffer with 10% ethanol. We used an injection volume of 2.5μL and flow rate of 0.5 mL/min.
Results and Discussion
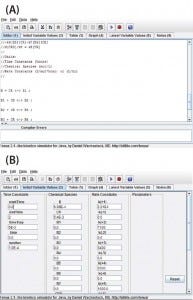
Figure 1: View of the program user interface (a) mechanism editor and (b) initial variable
values
Program Functionality: Figure 1a shows a screen capture of the Tenua mechanism editor with an example reaction, and Figure 1b shows the corresponding initial variable values. Mechanisms are input to the editor using simple notation. For instance, a bimolecular nonreversible reaction with the form shown in Equation 1 is input to the editor as Equation 2. Note that a double-headed arrow is used regardless of whether the reaction is reversible, and the reaction step is terminated with a semicolon. A positive value will be input for the forward rate constant k(1), and 0.0 is input for the reverse reaction k(–1). The initial concentrations of the reactants (Chemical Species) and integration parameters (Time Constants) are also input under initial variable values.
Equations 1–28:
Consecutive reactions with parallel consumption of conjugation reagent (as often encountered in bioconjugation) are input with reaction steps separated by a semicolon. As an example, a two-step reaction with the form shown in Equations 3 and 4 is input to the editor as Equations 5 and 6.
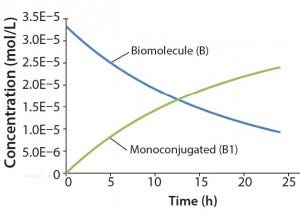
Figure 2: Reaction kinetics simulation for
monoconjugation (using parameters from
“Monoconjugation” section in the text)
Once the mechanism and variables are entered, the simulation can be started. The program will automatically generate and numerically integrate the resulting system of ordinary differential equations. It should be noted that the user must ensure that units for variables and rate constants are consistent. Results are output in both tabular and graphical form. Two text files are provided per example. The first is loaded into the mechanism editor, and the second is separately loaded into initial variable values.
Monoconjugation: For the first example, we consider a simple monocojugation reaction of the form shown in Equation 7, in which B denotes the biomolecule, CR denotes the conjugation reagent, and B1 denotes a monoconjugated biomolecule. This reaction leads to the ODEs shown as Equations 8–10.
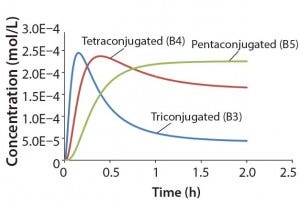
Figure 3: Reaction kinetics simulation for
multiconjugation with reagent deactivation
using parameters from Table I
For this example, we assume 1 g/L initial biomolecule concentration (MW 30000 Da) and a 5× molar excess of the conjugation reagent. We further assume the extent of reaction reaches ~70% after 24 h, thereby leading to the following rate constant: k1= 350 L/mol h. Figure 2 shows simulation results for this reaction. For simplicity, the concentration of the conjugation reagent is not shown.
Multiconjugation with Reagent Deactivation: We consider a scenario in which the biomolecule has more than one available conjugation site. In addition, we consider an undesired side reaction (e.g., deactivation of the conjugation reagent). The model and rate constants are based on previously published data from Buckley et al. for PEGylation of a growth hormone antagonist, as well as there are eight potential reactive amines and slow hydrolysis of the PEG reagent (16). The reaction mechanism is defined as shown in Equations 11–18, in which CRD is deactivated conjugation reagent, B1 denotes monoconjugated biomolecule, B2 is diconjugated, and so on. This reaction leads to the ordinary differential equations 19–28.
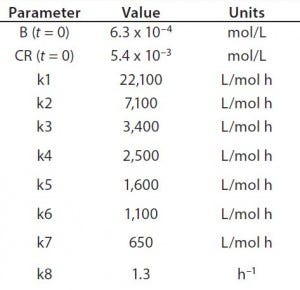
Table 1: Reaction parameters1 used for the multiconjugation simulation shown in Figure 3.
(1 From Reference 16)
Using the parameters shown in Table 1, Figure 3 shows the kinetic simulation for PEGamers 3–5 (B3, B4, and B5). Characteristic of consecutive reactions, it is interesting to note how the PEGamer 1–4 conjugation reaction intermediates increase to reach a maximum concentration before declining as they are consumed in the successive reaction. This result can clearly be seen for PEGamers 3 and 4 (B3 and B4) in Figure 3. This example illustrates the flexibility to simulate bioconjugation reaction models of greater complexity. In the next example, we consider a more complex process control strategy.
Multiconjugation with Linear Reagent Feed: As has been noted in the literature, fed-batch reagent addition can be used to control extent of conjugation and control distribution of higher-order reaction products (20). Such results are typically achieved using an addition pump to feed the conjugation reagent at a constant rate.
We can approximate this control strategy using a unimolecular reaction that converts a large excess of an inactive conjugation reagent precursor to the active form at a constant rate. If we consider a biomolecule with three reactive sites, we obtain the reaction mechanisms shown in Equations 29–32, in which CRP is the inactive conjugation reagent precursor. This reaction mechanism leads to the ODEs shown as Equations 33–38.
Equations 29–38:
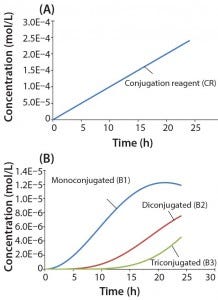
Figure 4: Reaction kinetics simulation for multiconjugation with linear reagent feed (a) conjugation reagent in the absence of a biomolecule and (b) mono, di, and tri conjugated species. Parameters used in the simulation are from the section, “Multiconjugation with linear reagent feed.”
In this example, we assume an initial concentration of 1 g/L for the biomolecule (MW 30,000 Da) and that all of the conjugation sites are equally reactive with rate constants of 500 L/mol h. Feed of the conjugation reagent will lead to a volume increase and dilution over time. For this example, we assume that the volume increase is small and can therefore be neglected. To simulate a linear reagent feed rate of 1 × 10-5 mol/h, we set the initial concentration of the reagent precursor to 100 mol/L and k1 value of 1 × 10-7 h-1. Figure 4a shows results for conjugation reagent (CR) generation as a function of time in the absence of further reaction with the biomolecule. Figure 4b shows the conjugation reaction products B1, B2, and B3 after 24 h of reaction. For this type of control strategy, the model affords a tremendous advantage in that many different feed rates and process conditions can be evaluated very quickly to find the optimal set of reaction parameters.
Table 2: Reaction parameters used for the multiconjugation simulation shown in Figure 5.
Modeling Amine PEGylation: To illustrate kinetic simulation of conjugation reaction data, we chose PEGylation of lysozyme as an example system using reaction conditions similar to those reported by Moosmann et al. (14). Figure 5 shows the experimental results obtained in our laboratory with the corresponding model fit. To describe the data (as observed previously) it was necessary to account for deactivation of the PEGylation reagent (14, 16). The reaction mechanism is comparable with that shown in the multiconjugation with reagent deactivation example, except for tetra PEGylation (including only k1–k4 and the deactivation term). Table 2 lists the parameters used in the simulation.
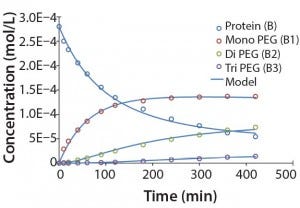
Figure 5: Experimental results for protein PEGylation and corresponding reaction kinetics
model. Parameters used in the simulation are from Table 2.
Figure 5 shows that the model can accurately capture the behavior of this complex reaction. For simplicity, the figure does not include the tetra PEGylated species because very small amounts were formed. Although not measured directly, our results suggest the half-life due to deactivation of the aldehyde PEG conjugation reagent is about 200 minutes. The data were fit in a manner similar to that described by Buckley et al., in which k1 was estimated from the protein concentration profile assuming a pseudo second-order reaction (16). Rate constants for higher-order PEGamers were estimated from the ratio at the end of the reaction.
Modeling Bioconjugation
Our work provides a flexible means to model bioconjugation reaction kinetics using a platform-independent, open-source chemical kinetics simulator. This approach does not require a detailed understanding of numerical methods or differential equations. Rather, all that is required is basic knowledge of chemical kinetics and the ability to define conjugation reaction mechanisms. We demonstrated the flexibility to model a number of different systems using examples of increasing complexity. Examples also included side reactions such as reagent deactivation and advanced control strategies such as fed-batch reagent addition.
Acknowledgments
We thank Bill Wang and Kripa Ram for their review of this manuscript. We thank Danny Wachsstock for implementation and maintenance of Tenua.
References
1 Trail PA, Bianchi AB. Monoclonal Antibody Drug Conjugates in the Treatment of Cancer. Cancer 11, 1999: 584–588.
2 Chapman AP, PEGylated Antibodies and Antibody Fragments for Improved Therapy: A Review. Adv. Drug Delivery Rev. 54, 2002: 531–545.
3 Harris JM, Martin NE, Modi M. PEGylation: A Novel Process for Modifying Pharmacokinetics. Clin. Pharmacokinet. 40, 2001: 539–551.
4 Gruber WC, Scott DA, Emini EA. Development and Clinical Evaluation of Prevnar 13, A 13-Valent Pneumocococcal CRM197 Conjugate Vaccine. Ann. N.Y. Acad. Sci. 1263, 2012: 15–26.
5 Poolman J, et al. Impact of the Conjugation Method on the Immunogenicity of Streptococcus pneumoniae Serotype 19F Polysaccharide in Conjugate Vaccines. Clin. Vaccine Immunol. 18, 2011: 327–336.
6 Junttila TT, et al. Trastuzamab-DM1 (T-DM1) Retains All the Mechanisms of Action of Trastuzumab and Efficiently Inhibits Growth of Lapatinib Insensitive Breast Cancer. Breast Cancer Res. Treat. 128, 2011: 347–356..
7 Ryan MC, et al. Targeting Pancreatic and Ovarian Carcinomas Using the Auristatin-Based Anti-CD70 Antibody–Drug Conjugate SGN-75. British J. Cancer. 103, 2010: 676–684.
8 Jennings GT, Bachmann MF. Immunodrugs: Therapeutic VLP-Based Vaccines for Chronic Diseases. Annu. Rev. Pharmacol. Toxicol. 49, 2009: 303–326.
9 Hermanson GT. Bioconjugate Techniques, 2nd Edition. Academic Press: New York, NY, 2008.
10 Harris JM, Chess RB. Effect of PEGylation of Pharmaceuticals. Nat.Rev. Drug Discovery. 2, 2003: 214–221.
11 Roberts MJ, Bentley MD, Harris JM. Chemistry for Peptide and Protein PEGylation. Adv. Drug. Delivery Rev. 64, 2012: 116–127.
12 Veronese FM, Pasut G. PEGylation, Successful Approach to Drug Delivery. Drug Discovery Today 10, 2005: 1451–1458.
13 Veronese FM. Peptide and Protein PEGylation: A Review of Problems and Solutions. Biomaterials 22, 2001: 405-417.
14 Moosmann A, et al. PEGylation Kinetics: A Standard Protein versus a Pharmaceutically Relevant Single-Chain Variable Fragment. Bioconjugate Chemistry 22, 2011: 1545–1558.
15 Maiser B, Dismer F, Hubbuch J. Optimization of Random PEGylation By Means of High-Throughput Screening, Biotechnol. Bioeng. 2013, DOI: 10.1002/bit.25000.
16 Buckley JJ, et al. PEGylation of Biological Macromolecules. Process Chemistry for the Pharmaceutical Industry. Gadamasetti, K, Braish T, Eds. CRC Press, Boca Raton, FL, 2008; 383–402.
17 Tenua: The Kinetics Simulator for Java; http://bililite.com/tenua.
18 Barshop BA, Wrenn RF, Frieden C. Analysis of Numerical Methods for Computer Simulation of Kinetic Processes: Development of KINSIM — A Flexible, Portable System, Anal. Biochem. 130, 1983: 134–145.
19 Oracle, www.oracle.com/technetwork/java/javase/downloads/index.html.
20 Fee CJ, Van Alstine JM. PEG-Proteins: Reaction Engineering and Separation Issues. Chem. Eng. Sci. 61, 2006: 924–939. •
Supplementary materials are posted online at http://bit.ly/Oct2014-bpiextra.
Corresponding author Alan K Hunter is principal scientist at MedImmune, Purification Process Sciences, One MedImmune Way, Gaithersburg, MD 20878; 1-301-398-4142; [email protected]. Wai Keen Chung is scientist II at MedImmune.
You May Also Like
