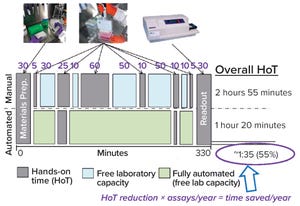
QA/QC
Identifying False Metabolite Measurements During Cell-Culture Monitoring Effective Application of the Multivariate Hotelling’s
QA/QC
Continued Process Verification: A Multivariate, Data-Driven Modeling Application for Monitoring Raw Materials Used in Biopharmaceutical Manufacturing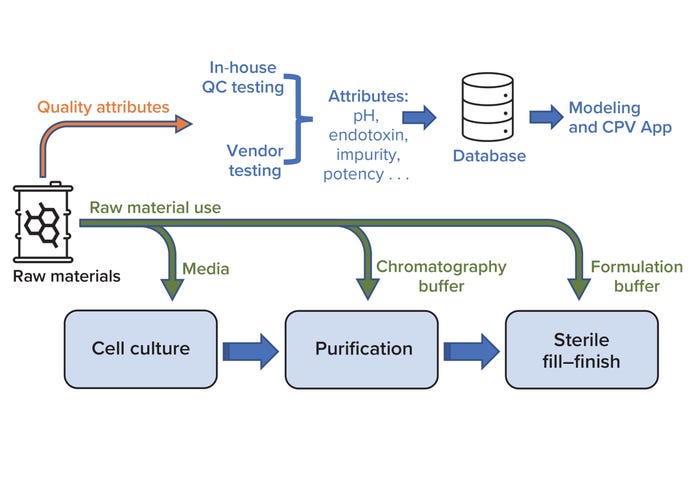
Biochemicals/Raw Materials